Bu kirigami | formülü kullanılarak bir daire bir kareye dönüştürülebilir. MİT Haberleri

Kirigami, pop-up kitapları yepyeni bir seviyeye taşıyor. Japon kağıt zanaatı, iki boyutlu bir kağıt yaprağını kısmen katlandığında karmaşık bir üç boyutlu yapıya dönüştürmek için kağıttaki kalıpları kesmeyi içerir. Bir sanatçının elinde kirigami, doğadaki yapıların, mimarinin ve daha fazlasının son derece ayrıntılı ve hassas kopyalarını üretebilir.

Bilim adamları ve mühendisler ayrıca kirigami’den ilham alarak kağıt kesmeden robotik kıskaçlar, gerilebilir elektronikler, su toplayan paneller ve diğer şekil değiştiren malzeme ve cihazlar tasarlamaya kadar ilkeleri uyguladılar. Çoğunlukla, bu icatlar sıfırdan tasarım ürünleridir. Mühendislerin, malzemeyi istenen bir şekilden diğerine dönüştürecek kesim modellerini belirleyecekleri bir plan yoktu – yani şimdiye kadar.

A Yeni çalışma Hesaplamalı Bilim Doğa Kirigami’den ilham alan herhangi bir 2B dönüşümü çözebilen genel bir algoritmik strateji sunar. Yöntem, yapılacak kesimlerin açısını ve uzunluğunu belirlemek için kullanılabilir, böylece tabaka, karmaşık bir genişleyebilir ağ gibi açılıp itildiğinde istenen bir şekilden diğerine dönüşebilir.

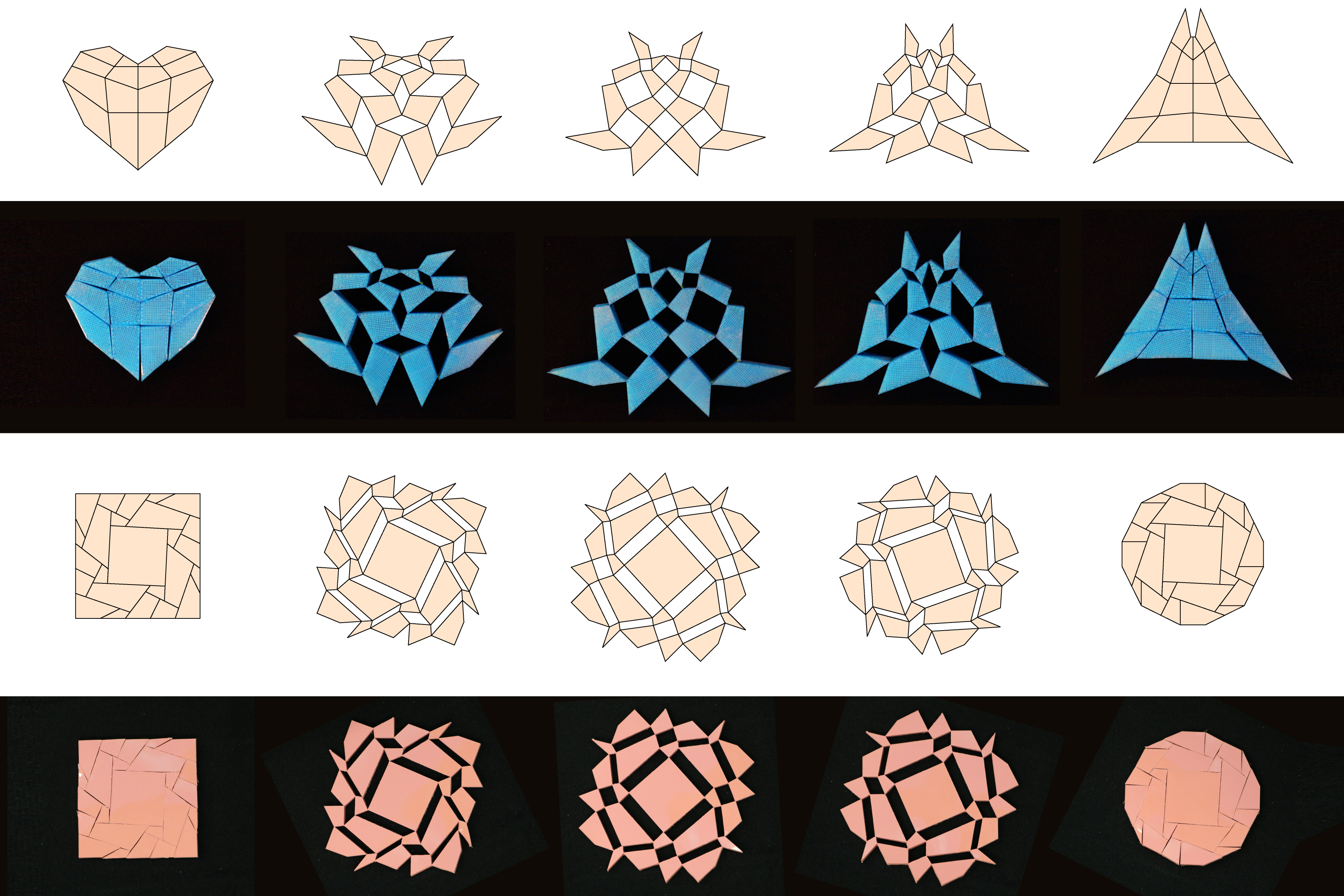
Araştırmacılar, yeni yöntemleriyle, kareye dönüşen bir daire ve kalbe dönüşen bir üçgen dahil olmak üzere bir dizi dönüştürülebilir 2D kirigami yapısı tasarladı ve inşa etti.

MIT’de doktora sonrası profesör ve uygulamalı matematik eğitmeni olan Gary Choi, “İnsanlar kare ve çemberden matematikteki imkansız problemlerden biri olarak bahsetti: Birini diğerine çeviremezsiniz” diyor. “Ama kirigami ile aslında kare şeklini daire şekline çevirebiliriz.”

Mühendisler için, yeni yöntem, belirli bir görevi yerine getirmek veya belirli alanlarda gezinmek için bir formdan diğerine dönüşecek bir robotun nasıl tasarlanacağı gibi çeşitli tasarım problemlerini çözmek için kullanılabilir. Binalar ve evler için akıllı kaplamalar gibi verimli malzemeler tasarlama potansiyeli de vardır.

MIT’de makine mühendisliği profesörü olan Caitlin Baker, “Düşündüğümüz ilk uygulamalardan biri bina cepheleri içindi” diyor. “Bu, güneş ışığını ve ultraviyole radyasyonu kontrol etmek ve çevrelerine uyum sağlamak için şekil değiştirebilen büyük, kirigami benzeri yüzler yapmamıza yardımcı olabilir.”

Baker ve Choi, Optiver’de kantitatif bir araştırmacı olan Levi Dowdy ve Harvard Üniversitesi’nde profesör olan L. Mahadevan ile birlikte yeni çalışmanın ortak yazarlarıdır.

arasındaki boşluk

Çalışma, ekibin Japon kağıt katlama sanatı olan kirigami ve origami üzerindeki önceki çalışmalarından ortaya çıktı.

Choi, “Kirigami ve origamide pek çok matematiksel bağlantı olduğunu bulduk” diyor. “Bu yüzden, insanların çok çeşitli desenler tasarlamasına yardımcı olabilecek bir matematiksel formül bulmak istedik.”

2019’da ekip, bir şekli diğerine dönüştürmek için gereken kesim modelini bulmak amacıyla kirigami için bir iyileştirme yöntemi tasarladı. Ancak Choi, yaklaşımın hesaplama açısından çok yoğun olduğunu ve belirli bir kaymayı başarmak için ideal bir model elde etmenin uzun zaman aldığını söylüyor.

2021’de araştırmacılar benzer bir origami sorunuyla karşılaştılar ve biraz farklı bir bakış açısıyla daha verimli bir strateji elde edebildiklerini gördüler. Ekip, bireysel kıvrımlardan oluşan bir model (bireysel kirigami parçalarına benzer şekilde) çizmek yerine, basit bir katlanmış tohumdan bir model oluşturmaya odaklandı. Plaka plaka çalışarak ve bitişik plaka katlandığında bir plakanın nasıl hareket edeceği gibi plakalar arasında ilişkiler kurarak, herhangi bir origami yapısının tasarımını planlamak için nispeten verimli bir algoritma türetebildiler.

Ekip, benzer bir yaklaşımın kirigami’ye uygulanıp uygulanamayacağını merak etti. Geleneksel kirigami’de, bir kağıt yaprağında kesim yapıldıktan sonra, kağıt kısmen katlanabilir, böylece ortaya çıkan boş alanlar üç boyutlu bir yapı oluşturur. Origami kıvrımları arasındaki paneller gibi, kesikler arasındaki boş alanlar ve bunların birbirleriyle olan ilişkileri, kirigami tasarımının daha verimli bir versiyonunu verebilir mi? Bu soru, ekibin yeni çalışmasının itici gücü.

Matematik Bağlantıları

Çalışma, iki boyutlu kirigami dönüşümlerine odaklanmaktadır. Araştırmacılar, her biri farklı açılarda ve boyutlarda kesilmiş, birbirine bağlı dörtgen karolardan oluşan bir mozaikten oluşan genel bir kirigami tasarımı düşündüler. Kavramsal mozaik tek bir şekil olarak başlar ve tamamen yeni bir şekil oluşturmak için ayrılıp bir araya getirilebilir. Buradaki zorluk, karolar arasındaki boş alanlara ve karolar çekilip tekrar bir araya getirildiğinde boşlukların nasıl değiştiğine bağlı olarak bir şeklin diğerine nasıl dönüşebileceğini açıklamaktı.

Baker, “Karoların kendileri sağlam ve değişmezse, aralarındaki boş alanlar hareket için bir fırsattır” diyor.

Ekip önce boş uzayın en basit temsiline, eşkenar dörtgen veya “dört çubuklu bağlantı” dedikleri şeye baktı. Eşkenar dörtgenin her bir tarafı, katı bir döşemenin bir şeridini veya kenarını temsil eder. Eşkenar dörtgenin her köşesi, kareleri birbirine bağlayan bir bağlantıyı veya menteşeyi temsil eder. Ekip, eşkenar dörtgenlerin kenarlarının uzunluğunu ve açısını değiştirerek, değişiklikler arasında boş alanın nasıl değiştiğini inceleyebilir.

Ekip, kademeli olarak daha büyük dört çubuklu bağlantı gruplarını inceleyerek, çubukların açısı ve uzunluğu, bireysel boşlukların şekli ve genel düzeneğin şekli arasındaki ilişkileri belirledi. Bu ilişkileri genel bir formülde çalıştılar ve bunun, iki boyutlu bir kağıdı istenen bir şekilden diğerine dönüştürmek için gerekli olan kesim modelini (açı ve uzunluk dahil) verimli bir şekilde belirleyebildiğini buldular.

Baker, “Böyle bir araç olmadan, Matlab’da bu sorunu kaba kuvvetle çözebilir veya tahmin edip kontrol edebilirim, ancak daireden kareye dönüşebilen bir şeyi elde etmek çok uzun zaman alırdı” diyor.

Simülasyonlarda ekip, formülün aslında daire şeklindeki bir mozaiği kareye ve hemen hemen her şekli istenen herhangi bir şekle dönüştüren bir karo deseni bulabileceğini buldu.

Ekip, formül tasarımlarını fiilen gerçekleştirmek için iki üretim yöntemi geliştirdi. Kısa süre sonra, aktarılabilir mozaikler yapmaktaki asıl zorluğun, karo eklem menteşeleri olarak hareket edecek doğru malzemeyi bulmak olduğunu anladılar. Eklemler sağlam ve kolay bükülebilir olmalıdır.

“Gerilimde bu kadar güçlü, yırtılmaya karşı dayanıklı, ancak neredeyse hassas bir menteşe gibi sıfır bükülme yarıçapına sahip olabilen şey nedir?” diye düşündüm. Bekir diyor. Ve yanıtın doku olduğu ortaya çıktı.

Ekip, küçük kumaş şeritlerini dört taraflı plastik karolara gömmek için iki yöntem – 3D baskı ve kalıp döküm – kullandı ve karoları birbirine yaslamalarına izin verirken birbirine sıkı bir şekilde yapıştırdı. Ekip, bu iki yöntemi kullanarak kareye dönüşen dairelerden oluşan bir mozaiğin yanı sıra daha karmaşık kalp şekillerine dönüşen basit üçgenlerden oluşan bir mozaik oluşturdu.

Choi, “Temelde herhangi bir iki boyutlu şekle girebiliriz” diyor. “Matematiksel formülümüzü kullanarak bu kusursuz. Şimdi bunu 3D kirigami’ye genişletmek istiyoruz.”